A recent study has emerged unveiling the absolute speed of a wave traveling through solids to be 22.4 km per second (22.4 miles per second). The researching physicists concluded that when combining the constant of fine structure and the proton to electron mass ratio in one singular equation, a new dimensionless constant is formed representing the upper bound for the speed of sound. Throughout this piece, I plan on breaking down the complex algorithms and jargon to make it more approachable to read. In addition, I want to shed light on how the physical sciences can correlate to the realm of communication by intertwining the two and showing how with equations such as this, it can be communicated to other disciplines. This is a dramatic breakthrough in the physics world and needs to be understood as it could impact the future of how we understand our natural world.
To start, the overall focus of this study was to come up with an equation that can be used to find the upper bound for the speed of sound. In other words, they found the maximum possible speed that sound can travel through solids and liquids. Initially, Einstein’s theory of special relativity calculated that a wave could travel at peak velocity at 300,000 km per second (186,000 miles per second). However, this is the velocity traveling through the air and not solids or liquids (which drastically reduces the speed of a sound wave). Up until now, this cap of speed was simply not able to be calculated. This finding allows physicists to understand more about how waves interact with the world. It can be as practical as waves hitting a building’s structure or waves impacting other planets such as gas giants like Jupiter. As mentioned, this is a complex equation that needs to be broken down into sections in order to understand. To start, knowledge of a simple wave must be known.
Within the realm of physics, a wave is the displacement of particles that move in a path like waves seen in water. Waves can be broken down into three main categories: mechanical, electromagnetic, and matter (see image below for physical example). The two that are critical to understanding this new study are mechanical and electromagnetic. Mechanical waves require an oscillation of matter to transfer energy in a wave pattern. These can be experienced in the form of waves in the ocean or soundwaves. The only caveat to this type of wave is the oscillation of matter acting as a medium; mediums being a way to carry the wave onward such as the air with sound waves. Electromagnetic waves contrast mechanical as they do not require a medium and instead move through a vacuum (a space devoid of matter). As mentioned, these two types of waves are needed to understand the process of finding the upper bound for the speed of sound. To start this study, two main constants need to be present.
The two constants that are needed for this study are the constant of fine structure and the proton to electron mass ratio. The constant of fine structure is used to explain the strength of the electromagnetic force and offers a way to compare how electrons (negative charge particle) and photons (light particle) interact. The actual value of this constant is surprisingly simple as 1/137. This is important to the equation as the relationship between matter and light (the purpose of this constant) is needed to multiply with the proton to electron ratio. The proton to electron ratio is simply the mass of a proton compared to the mass of an electron. It is a common constant that is seen throughout various equations. By this constant, the ratio of mass is 1,836.153. In the found equation, this constant was used to multiply against the constant of fine structure. Kostya Trachenko, physicists who worked on this ratio, was quoted saying, “If you change these constants by a few percent, then the proton might not be stable anymore, and you might not even have the processes in stars resulting in the synthesis of heavy elements”. Thankfully in this equation, the ratio is not changed at all. Now that the different parts of the equation have been explained, the discovered equation can be explained.
So, the equation the physicists came up with is a combination of all the parts described earlier. Their research unveiled this equation:
 Equation from: Science Advances
Equation from: Science Advances
First and foremost, the equation’s structure comes from an alteration to Einstein’s theory of special relativity. Now each symbol represents a constant/number:
Vu = upper bound for the speed of sound
C = speed of light
α = constant of fine structure
(me/2mp) = proton to electron ratio
As mentioned earlier, the constant of fine structure is multiplied by the proton to electron ratio (this portion is up to the ½ as that is part of Einstein’s theory of special relativity). These two multiplied constants offer the constant for the upper bound for the speed of sound, Vu. With this, there is no set-in-stone unit to this equation as Vu depends on the type of matter the sound wave is traveling. Thus, there is a range for the upper bound for the speed of sound which comes out to .6 to 2.4 km per second. On a side note, the constant for the upper bound for the speed of sound is over the speed of light, C, as the speed of sound coincides with the speed of light. For example, lightning is always seen before heard.
Now how does this have anything to do with communication you might be asking? Well this equation can tie into other disciplines such as architecture or astronomy. Within the realm of architecture, architects can use the equation to study how waves effect buildings. This is critical in areas such as in California where seismic waves from earthquakes constantly effect building foundations. The equation can aid these architects to determine the proper strength/resistance these buildings need to stay in tact. In astronomy, astrologists can use the equation to determine how certain gaseous planets function.
In one test, they concluded that further research can be continued on waves passing through other planets. One main example they displayed is how waves could react with gaseous planets such as Jupiter. In the study, the constant worked with the density and pressure of gasses found on the planet, specifically atomic hydrogen. This allowed the astrologists to get a deeper understanding of the planet and unveil more characteristics that were previously left to the unknown.
This equation is a massive breakthrough for more than just physicists. It is a breakthrough that can span over countless disciplines. It allows for further investigation to occur within the physical world on Earth and the cosmic world of space. This only begs the question as to what can be discovered next and how far this constant can take us in understanding the natural world as we know it.
 Image from: Pixabay
Image from: Pixabay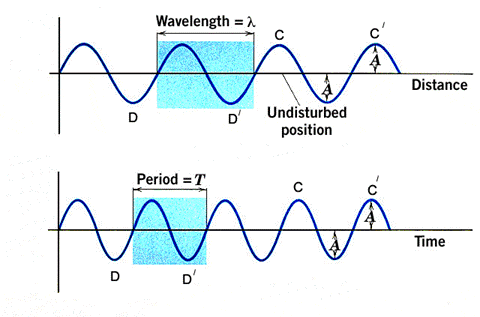 Image from: Wikimedia Commons
Image from: Wikimedia Commons Image from: Wikimedia Commons
Image from: Wikimedia Commons